플로이드와샬 알고리즘 (Floyd Warshall)
최단거리를 구하는 알고리즘이지만, BFS가 한 정점에서부터 모든 정점으로의 최단거리라면 플로이드와샬은 그래프에서 모든 정점 사이의 최단거리를 구하는 것이 가능하다. 그래프의 간선들 중 음의 가중치가 존재해도 실행된다. 시간 복잡도는 3중 for문으로 인한 O(V^3)을 가진다. 많은 시간이 소요되지만 이 알고리즘을 이용해야하는 상황이 존재한다.
플로이드 와샬의 기본 개념은 i에서 출발해 j로 가는 경로의 가중치를 저장하는 2차원 배열을 채우는데, i를 출발해 j로 바로 가는 것보다 k를 거쳐 j로 가는 게 효율적일 경우(저렴할 경우) 해당 값을 갱신해준다. k의 값을 가장 바깥 for문에서 반복해주므로 하나의 경유지 k만 거치는 것뿐만 아니라 여러 경유지를 거치는 경로또한 포함한다.
# k : 경유지
for k in range(1, v+1):
# i : 출발지
for i in range(1, v+1):
# j : 목적지
for j in range(1, v+1):
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])플로이드 와샬 알고리즘의 예시로 아래 플로이드 문제(link)를 풀어보자.
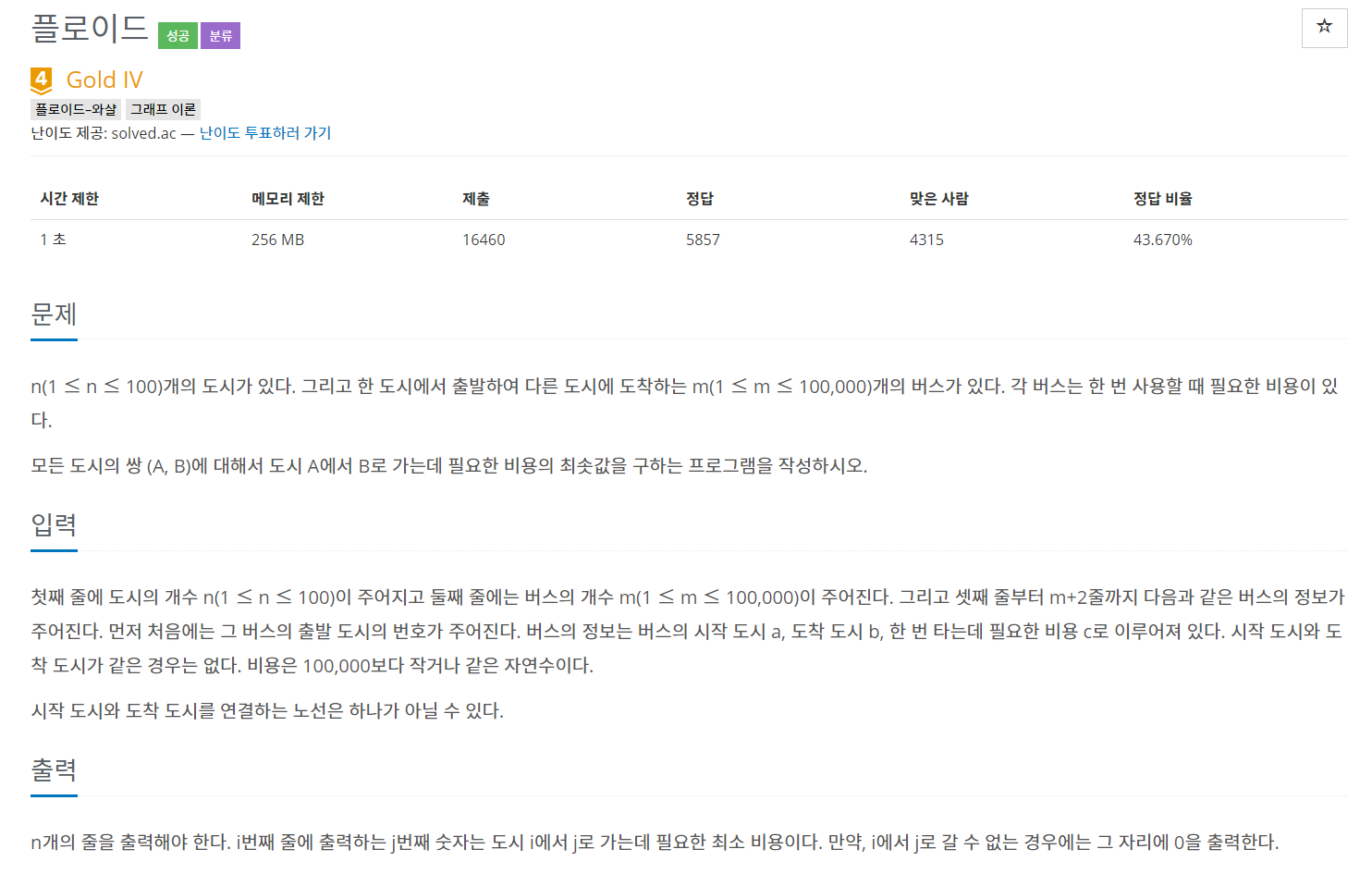
가장 기본적인 플로이드 와샬 알고리즘을 이용한 문제이다. 주의할 점은 최소 비용을 구하는 것이기 때문에 2차원 배열은 큰수, 즉 INF로 초기화한다.
from sys import stdin
from math import inf
n = int(stdin.readline())
m = int(stdin.readline())
# 이동 최소비용을 저장할 2차원 배열
cost = [[inf] * n for _ in range(n)]
for _ in range(m):
a, b, c = map(int, stdin.readline().split())
cost[a-1][b-1] = min(cost[a-1][b-1], c)
# 플로이드 와샬 알고리즘 적용
k in range(n):
cost[k][k] = 0
for i in range(n):
for j in range(n):
cost[i][j] = min(cost[i][j], cost[i][k]+cost[k][j])
# 결과 출력
for row in cost:
for i in range(n):
# 갈 수 없는 경로인 경우, 0 출력
if row[i] == inf:
row[i] = 0
print(row[i], end=" ")
print()